In everyday language, we often use the term ‘Work'. A teacher teaching a class, a mom cooking food, or a farmer plowing the field, all are said to be working. In physics, work and energy have precise meanings which must not be confused with their everyday meanings. For example, a person who can put in long hours of work is said to have large stamina or more energy. Or when we lift boxes of some weight, we get tired and hungry. We need to eat food to obtain energy. So, work and energy are related to one another.
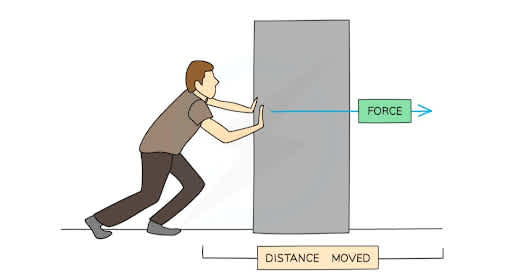
man-pushing
We define work W as the energy transmitted to or from an object using a force acting on the object. Energy transferred to the object is positive work and energy transferred from the object is negative work. Therefore, ‘doing work' is nothing but the act of energy transfer. Work is said to be done by a force when the body is displaced actually through some distance in the direction of the applied force. It is denoted by W.
However, when there is no displacement in the direction of applying force, no work is said to be done or work done is considered zero.
FORMULA OF WORK
Suppose a constant force F acting on a body develops a displacement ‘s’ in the body along the x-direction. As shown in the figure, if θ is the angle that F makes with the positive direction of the displacement, then the two rectangular components of F are:
Fx in the direction of s where Fx= Fcosθ
Fy in the direction of s where Fy = Fsinθ
The component Fy does no work as the body does not move. All the work is done by component Fx.
W= Fx × s = Fcosθ × s
W = (Fcosθ) s

graph-2
Hence, the work done by the force is the product of the component of the force in the direction of displacement and the magnitude of displacement.
Keep in memory – When we calculate the work done by a force, we only use the force component along with the object’s displacement. The force component perpendicular to the displacement of the object does not work.
![man-image]()
man-image
The formula for work can be rewritten as W = F.S. Work is a scalar quantity which means it has magnitude only and no direction. However, work done by a force can be positive, negative, or zero.
DIMENSIONS AND UNITS OF WORK
As work = force × distance, where dimensions of force- (M¹L²T-2).
W = [M¹L¹T-2] × L
W = [M¹L²T-2], This is the dimensional formula of work.
The units of work are of two types:-
Absolute units — The absolute unit of work in the cgs system is Erg.
And the absolute unit of work in the SI system is the joule.
2. Gravitational units — The gravitational unit of work on the cgs system is g-cm.
And the gravitational unit of work on the MKS system is kg-m.
NATURE OF WORK DONE
Although Work Done is a scalar quantity, its value may be positive, negative, or even zero.
a) Positive work:-
As W= F.s = Fs cosθ, when θ is acute (<90°), cosθ is positive. Hence, the work done is positive.
For example-
When a body falls freely under the action of gravity, θ= 0°, cos θ = cos 0° =+1.
When a spring is stretched, work done by the stretching force is positive.
b) Negative work:-
As W= F.s = Fs cosθ, when θ is obtuse (>90°), cosθ is negative. Hence, the work done is negative.
For example-
When a body is thrown up, its movement is hindered by gravity. The angle θ =180°.
As cos θ = cos 180° = -1. Hence, work done by gravity on a body that is moving upwards is always negative.
When brakes are applied on a moving vehicle, work done by the force is negative.
c) Zero work:-
When force or displacement or both are zero, work done W= Fs cosθ is zero. Again, when the angle between F and s is 90° then cosθ= cos90°= 0. Therefore, the work done is zero.
For example-
When a coolie carrying a load on his head moves on a horizontal platform, θ = 90°. Motion is at 90° to the force applied. Therefore, work done by a coolie is zero.
Tension in the string of a simple pendulum is always perpendicular to the displacement of the bob. Therefore, work done by tension is always zero.

graph
WHAT IS THE WORK DONE BY A VARIABLE FORCE?
A variable force is a force whose direction or magnitude or both changes with time. It is interesting to realize that the forces we experience every day are mostly variable. A constant force is rare.
In the case of variable force, work done is calculated by the integration method. The formula of work done by a variable force is
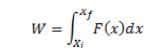
formulae-1
Example:- For this plot given below the formula will be:-
W= Area ABCDA
And hence work done by a variable force is numerically equal to the area under the force curve and the displacement axis.

work-done
CONSERVATIVE FORCES
A force is said to be conservative if work done by or against the force in moving a body depends only upon the initial and final positions of the body. It does not depend upon the nature of the path followed in between the initial and final positions. The total energy is constant. This means that work done by or against a conservative force in moving a body over any part between fixed initial and final positions will be the same. And the work done is recoverable in the case of conservative forces. A gravitational force is an example of a conservative force.
How gravitational force is a conservative force?
Gravitational force is a conservative force as work done against gravitation is always conserved. This can be understood by taking an example of a ball thrown vertically upward against gravitation.
Consider Work done against the gravity
W' = -mgh, where
mass of the ball = m
Height = h
Acceleration due to gravity = -g
Consider the work done by the ball when the ball falls back from the same height
W”= mgh
Total work done= W'+ W”
= -mgh + mgh
= 0 (zero)
Hence, the total work done throughout the traveling of the ball or any object will be zero. Because the gravitational force is conservative. It follows the property that Work done only depends on the final and initial position of the object, not over the path followed.
Other examples of Conservative forces are electrostatic force and magnetic force.
Properties of Conservative Forces:-
In moving a body from one position to the other, Work done by or against a conservative force depends only on the initial position and final position of the body.
Work done by or against a conservative force does not depend upon the nature of the path followed by the body.
In a closed path, work done by or against a conservative force is always zero. This is because the initial and final position overlaps with each other in a circular path.
NON-CONSERVATIVE FORCES
A force is non-conservative if work done by or against a conservative force depends upon the path followed by a moving body. The work done in the case of non-conservative force is not completely recoverable. They cause a loss of mechanical energy from the system. Also in a non-conservative force, energy is dissipated through heat. Frictional force can be a good example of a non-conservative force.
How frictional force is a non-conservative force?
Consider a body moving from position A to another position B on a rough table. Work done against frictional force(W) will depend on the length of the path between A and B and also on the positions A and B.
Further, if the body is then brought back to its initial position A, from the same path. Now again, the work(W) has to be done against the frictional force which opposes the motion always. Hence, net work done against the frictional force in moving a body over a round strip is not zero. It is numerically equal to 2W.
Wclosed path ≠ 0
Ei = total value of initial energy, Ef = total value of final energy
Then, Ei - Ef = 2W
Other examples of non-conservative forces are viscous force, air resistance, tension, etc.
Properties of non-conservative forces:-
Work done by or against a force depends on the nature of the path followed by the body.
Energy is dispersed by heat energy.
Example- When we rub both our hands with one another, we begin to feel the heat being produced which is due to friction between the two hands.
In a closed path, work done by or against a non-conservative force is never zero.
Non-conservative force is used for transforming the macroscopic motion into microscopic motion.
The work done by or against non-conservative force appears in some other forms of energy like heat, sound, light energy, etc.
