A triangle suggests that it's a curve that includes a three line of segments. A triangle has three aspect fashioned by angular . the 2 purpose of a triangle wherever meer is named a vertex. the bottom of a triangle will anyone of triangle 3 sides, it's typically bottom one. The angular fashioned at the vertices is named a angles of the Triangle. the purpose of traingle intersection of the edges is named the vertices of the Triangle. All triangle have three sides and three corners. The add of triangle of internal aspect is often 180° does not matter however a triangle area unit created. The triangle are often forever be a split into a pair of right triangles does not matter however was triangle area unit created. The length of triangle on any aspect is shorter than the add of a different 2 sides.
There area unit 3 styles of a triangle it's supported the aspect Equilateral Isosceles Scalene
Types of Triangles:
1) Equilateral triangle:
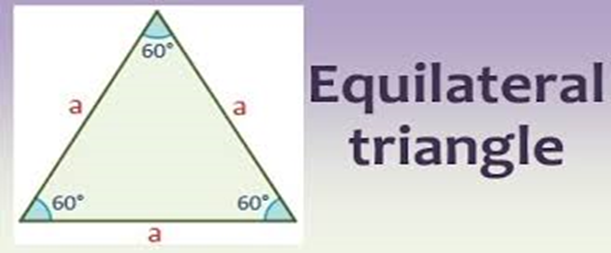
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60 degrees.
Area is (√3/ 4) x (side of equilateral triangle) ² The Internal angle of an equilateral triangle is 60°.
2) Right isosceles triangle:
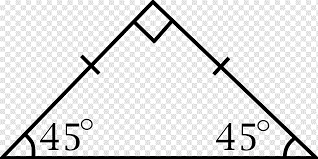
Right isosceles triangle
The Right Triangle always has one Right angle with a 90 ° angle. If the Right Triangle is Isosceles, the two sides of the same length are opposite the wrong. A right triangle with the two legs (and their corresponding angles) equal. An isosceles right triangle therefore has angles of 45 degrees, 45 degrees, etc. Thus, in an isosceles right triangle, two legs and the two acute angles are congruent.
The Formula of a right isosceles triangle is
Using base and Height = A = ½ × b × h Using all three sides = A = ½ [√(a2 − b2 ⁄4) × b]
Using the length of 2 sides and an angle between them= A = ½ × b × c × sin(α)
3) obtuse isosceles triangle
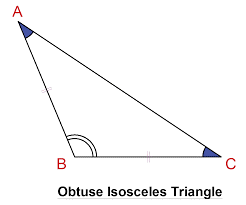
obtuse isosceles triangle
An isosceles obtuse triangle is a triangle in which one of the three angles is obtuse (lies between 90 degrees and 180 degrees) and the other two acute angles are equal in measurement. One example of isosceles obtuse triangle angles is 30°, 30°, and 120. In an isosceles triangle, two sides are the same length. An isosceles triangle may be right, obtuse, or acute.
The Formula of obtuse isosceles triangle is the area of an obtuse isosceles triangle can be calculated by using the formula: Area = 1/2 × base × height square units. The base is the side opposite to the vertex from where the height is drawn or measured.
4) Acute Isosceles Triangle
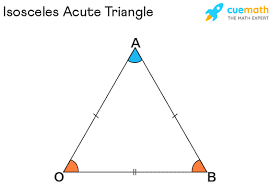
Acute isosceles Triangle
An isosceles acute triangle is a triangle in which all three angles are less than 90 degrees and at least two of its angles are equal in measurement. One example of isosceles acute triangle angles is 50°, 50°, and 80. Isosceles triangles always have two equivalent interior angles, and all three interior angles of any triangle always have a sum of degrees. Since this is an acute isosceles triangle, all of the interior angles must be acute angles.
The Formula for the acute angle triangle is the area of an acute isosceles triangle that can be calculated by using the formula: Area = 1/2 × base × height square units.
5) Right Scalene Triangle
Right scalene triangle
When one of the three angles measures 90 degrees and the angles or lengths of other two sides are not congruent, then the scalene triangle is called right scalene triangle. A right scalene triangle is a triangle that contains the properties of both the right triangle and scalene triangle. It comes in the category of both right triangles and scalene triangles. One of its angle’s measures 90°and all the sides and angles are different in measurements.
The area of a scalene right triangle can be calculated by using the formula: Area = 1/2 × base ×height. The perpendicular of the right scalene triangle can be taken as the height and the side adjacent to it other than hypotenuse is the base.
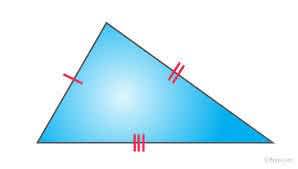
6) Obtuse Scalene
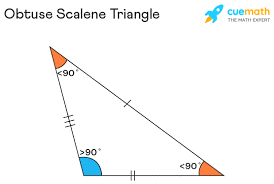
Right scalene triangle
In geometry, an obtuse scalene triangle can be defined as a triangle whose one of the angles measures greater than 90 degrees but less than 180 degrees and the other two angles are less than 90 degrees. All three sides and angles are different in measurement. A scalene triangle can be acute-angled or obtuse-angled or right-angled. An obtuse triangle is any triangle that has an obtuse angle. ... A scalene triangle is one which have all three sides of a triangle of different lengths and all three angles of different measures.
The Formula of obtuse angle triangle is the formula for a scalene obtuse triangle area is (1/2) × b × h square units
DESCRIPTION OF TRIANGLE
1) The sum of all the angles of a triangle (of all types) is equal to 180°. 2) The sum of the length of the two sides of a triangle is greater than the length of the third side. 3) In the same way, the difference between the two sides of a triangle is less than the length of the third side. 4) A triangle is a closed shape with 3 angles, 3 sides, and 3 vertices. A triangle with three vertices P, Q, and R is represented as △PQR. The most commonly seen examples of triangles are the signboards and sandwiches that are in the shape of a triangle.
FAQS OF TRIANGLE
The add of all the interior angles of a triangle is often one hundred eighty degrees. and notwithstanding however the Triangle is to be created. A triangle will forever be a split into the 2 right triangles and notwithstanding a way to be the Triangle is coA triangle has the 3 sides, 3 vertices, and therefore the 3 angles . The add of the 3 interior angles of a triangle is often one hundred eighty degrees . The add of the length of the 2 aspects of a triangle is often larger than the length of the third side educated . One of the primary shapes studied in pure mathematics . Triangles area unit significantly vital as a result of absolute polygons with four, five, six or n sides are often rotten into the triangles.
CONCLUSION OF TRIANGLE
CONCLUSION OF TRIANGLE
A triangle has three sides, three vertices, and three angles. The sum of the three interior angles of a triangle is always 180°. The sum of the length of two sides of a triangle is always greater than the length of the third side. f two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. They are one of the first shapes studied in geometry. Triangles are particularly important because arbitrary polygons (with 4, 5, 6, or n sides) can be decomposed into triangles. All angles of an equilateral triangle are equal. A triangle cannot be constructed from a three-line segment if any of them is longer than the sum of the other two. The triangle inequality theorem states that any side of a triangle is always shorter than the sum of the other two sides. how the triangle is coA triangle has three sides, three vertices, and three angles. The sum of the three interior angles of a triangle is always 180°. The sum of the length of two sides of a triangle is always greater than the length of the third side Instructed.